摘 要:研究单机带时间 B-约束的排序问题,即在任意单位时间区间[x,x +1)内至多允许加工 B 个工件,目标函 数是极小化工件的最大完工时间.分析了 B=2 时最优排序的结构与性质,设计了 O(n log n)时间的启发式算法. 当工件数较少(≤6)时,证明了该算法的最优性.

关 键 词:单机排序;时间约束;最优性;启发式算法

0 引 言

最近,BRAUN 等[1]提 出 了 如 下 带 时 间 约 束 (time restrictions)的单机排序问题:设有 n 个工件 需在单台机上加工,工件 i 的加工时间为p i ≥0,其 中加工时间为 0 的工件称为零工件.工件 i 可以在 任意长度为p i的时间区间[α,α+pi)内加工并完成, 其中α≥0 为其开工时刻.除零工件外,同一时刻至 多允许 1 个工件在机器上加工.同时,机器在加工 过程中还需满足时间 B-约束,即在任意单位时间区 间[x,x+1)内至多允许加工 B 个工件,其中 B 为给 定正整数.该问题可看作一类带资源约束的排序新 模型[2],如机动车自动导引、医院 手 术 排 程 等[3-4].

BRAUN 等[1]以极小化工件最大完工时间为目标函 数,证明了当 B 为输入值时问题是 NP-难的;当 B 为常数时,对求解问题的 LS 算法进行了渐近最坏 情况分析,特别是当 B =2 时证明了 LS 算法的渐近 紧界为 4/3.BRAUN 等[5]分析得到 LPT 算法的渐 近最坏情况界为 2 -2/B .ZHANG 等[4]改进了上 述结果,给出了 B =2 时的渐近最优算法以及 B ≥5 时的渐近紧界为 5/4 的改进算法. BRAUN 等[1]将 B 为常数情 形 的 计 算 复 杂 性 作为公开问题,ZHANG 等[4]猜测 B =2 的情形属 于 P 问题(多项式时间可解问题).本文分析 B =2 时最优排序 的 结 构 与 最 优 解 的 性 质,并 在 此 基 础上设计了一个时间复杂度为 O(n log n)的启发式 算法;当工件数较少(≤ 6 )时,证 明 了 该 算 法 的 最 优性.

1 最优排序的结构与性质

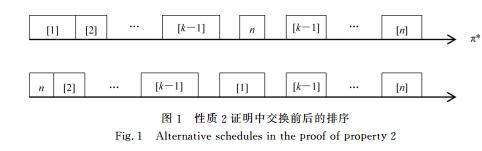
假设工件的加工时间满足p 1 ≥p 2 ≥…≥p n .为 方便叙述,下文仅用加工时间表示对应工件.由文 献[1,4]的结论,不妨假设p 1 ≤1.根据文献[1],一 个可行排序可以用工件或其加工时间的排列π来表 示,如π=(p [1],p [2],…,p [n]).具体地,首先从 0 时 刻开始加工工件p [1],在加工第 i 个工件p [i]时,为满 足时间 B-约束,其开工时间既不能早于p [i-2]的完 工时间后一个单位时间,也不能早于p [i-1]的完工时 间,每个工件都尽可能早开工,称上述由排列产生可 行排序的规则为 LR 规则.类似地,可以从排列中 最后一个工件自右向左产生可行排序,称为 RL 规 则.从排列中任意一个工件向左右两边产生可行排 序的规则,称为 M 规则.根据时间约束的定义及上 述规则,显然有以下性质:

结果

研究了单机带时间 B-约束的排序问题,分析了 B =2 时最优排序的性质并设计了启发式算法 W, 证明算法在工件数 n≤6 时是最优的.当 n≥7 时,算 法 W 是渐近最优的,但当 n=7 时,算法也非绝对最 优,因此猜想 B =2 时带时间约束的单机排序可能 是 NP-难的,未来研究方向是设法给出该问题的计 算复杂性证明.