摘要：研究了平面波斜入射空间光调制器（SLM）时完美涡旋光束的变化。结合螺旋相位与锥透镜透过率函数 设计相位掩模板，在 SLM的傅里叶平面上产生完美涡旋光束。所产生的涡旋性质通过调控完美涡旋光束 ±1 级干涉得到了验证。改变平面波照射在 SLM上的入射角，完美涡旋光束离心率与平面波入射角为线性函数 关系，相关系数高达 0.986 72。此外，随着平面波入射角增大，完美涡旋光束总光强也随之变弱。

关键词：物理光学；光场调控；完美涡旋光束；空间光调制器；线性相关

0 引言

由于涡旋光束呈螺旋形相位分布且中心光强为零，因此，在微粒操控 、量子信息编码 、图像 处理等多个领域中得到了广泛的应用。然而，使用传统方法生成的涡旋光束，其光环半径随拓扑荷 值的增加而增大，这就使得涡旋光束在耦合、传输等领域的应用变得极为困难。

为了解决该问题，2013 年，文献[10]首次提出了完美涡旋光束的概念，即中心亮环半径不随拓扑荷 值增加而增大的涡旋光束，并提出了一种实验生成完美涡旋光束的技术，但是其生成的完美涡旋光束伴 随有额外的杂散光环。同年，文献[11 ]提出了一种利用锥透镜产生完美涡旋光束的生成技术，消除了 次级亮环的影响并进行了微粒操控，但实验中需要更换锥透镜来获得不同半径的完美涡旋光束。随后， 文献[12]基于计算全息技术，将锥透镜与涡旋项编码到一个全息掩模板上，实现了不同半径完美涡旋 光束的实时在线调控。2016 年，文献[13]比较了多种完美涡旋光束生成方案，提出了一种生成完美涡 旋光束的最佳相位元件。

上述技术均是从完美涡旋光束理论近似公式出发，逐渐完善完美涡旋光束的生成技术。但对于一 种光束的生成来说，决定光束质量的不仅仅是所使用表达式的近似程度，实验光路的设计对光束的生成 同样有很大影响。然而，关于实验光路的设计对完美涡旋光束的影响还未见报道。因此，本文使用文 献[1 2]提出的锥透镜与涡旋项编码成一个掩模板，生成完美涡旋光束的技术方案，分析了被调制光 束入射角对生成完美涡旋光束的影响，得到了被调制光束入射角对完美涡旋光束离心率及光强的定 量关系。

1 完美涡旋光束的理论基础

2 实验装置

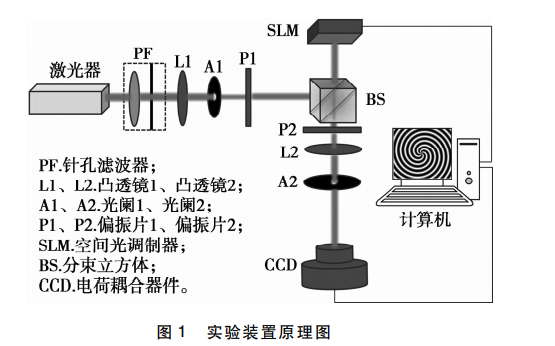
基于上述理论生成完美涡旋光束所对应的 实验装置原理图，如图 1 所示。由激光器发出 的光 束 经 针 孔 滤 波 器 （pinhole filter，PF）整 形 后，通过凸透镜 L1 与光阑 A1 得到平面波，之后 经过偏振片 P1 起偏后通过分束立方体 （beam splitter，BS）照射在写有相位掩模板的空间光调 制器 （spatial light modulator，SLM）上。在 SLM 的衍射空间经偏振片 P2 检偏后再现贝塞尔-高 斯光束。贝塞尔-高斯光束经凸透镜 L2 进行傅 里叶变换后产生完美涡旋光束，再经过光阑 A2，由位于透镜焦平面处的电荷藕合器件（charge coupled device，CCD）相机记录生成的完美涡旋光束光强分布。实验中，需将 SLM、CCD 相机放置于凸透镜 L2 的焦平面处。采用的激光器是北京镭志威光电技术有限公司生产的 LWGL532-100 mW-SLM型连续波 固体激光器，其功率为 50 mW，波长为 532 nm。使用的 CCD 相机为 Basler acA1600-60gc 型彩色相机，其 像素尺寸为 4.5 μm ×4.5 μm，分辨率为 1 600 pixel ×1 200 pixel。空间光调制器 （型号 HOLOEYE PLUTO-VIS-016）的像素尺寸为 8 μm ×8 μm，填充因子为 90％。

3 结果与分析

从两个方面证明所生成的光束为完美涡旋光束：（Ⅰ）光束半径独立于拓扑荷值；（Ⅱ）光束中含有 螺旋相位。

当锥透镜锥角 α＝0.085°时，使用上述实验装置生成了不同拓扑荷值时的完美涡旋光束，如图 2 所 示。拓扑荷值 m 分别为 2，4，6，8。

由图 2 可以看出：所生成光束为一个光强较为均匀的圆环，证明了实验生成的完美涡旋光束质量较 好。值得注意的是，完美涡旋光束光环外围有其他较暗的光环，其主要原因为使用锥透镜的方法生成完 美涡旋光束是一种近似方法，因此伴随有杂散光生成[13] 。此外，随着拓扑荷值的增加，光束亮环半径几 乎不变，定性地证明了所生成光束为完美涡旋光束。

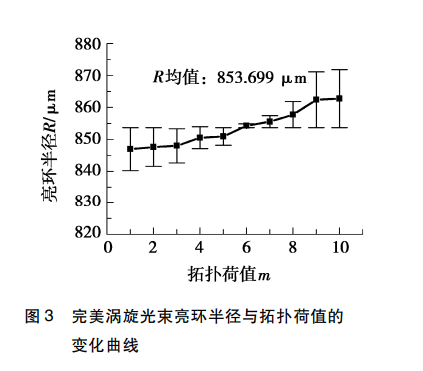
为了进一步定量分析，绘制了完美涡旋光束亮环半径 与拓扑荷值的变化曲线，如图 3 所示。图 3 中，误差线代表 的是完美涡旋光束光环半径的绝对误差值。由图 3 可以看 出：实验生成的完美涡旋光束并不像理想状态下的完美涡 旋光束一样半径完全独立于拓扑荷值。在一定范围内实验 得到的完美涡旋光束半径随着拓扑荷值的增加而增加，然 而其增加量较小，最大相对误差仅为 0.96％。因此，该实验 生成的完美涡旋光束近似为理想状态下的完美涡旋光束。

为了验证生成的完美涡旋光束含有螺旋相位，通过相 移技术[16] 调控 SLM光束 ±1 级衍射得到完美涡旋光束相干 叠加，干涉条纹如图 4 所示。由图 4 可以看出：不同拓扑荷 值的完美涡旋光束均产生了螺旋条纹，其条纹数为拓扑荷值的 2 倍，证明了所生成的完美涡旋光束具有 螺旋相位[17] 。

上述完美涡旋光束的产生与验证均是在保证平面波垂直入射 SLM时的实验结果。下面探究平面 波照射在 SLM上的入射角 θ对生成完美涡旋光束的影响。不同平面波入射角时，完美涡旋光束亮环光 强图如图 5 所示。

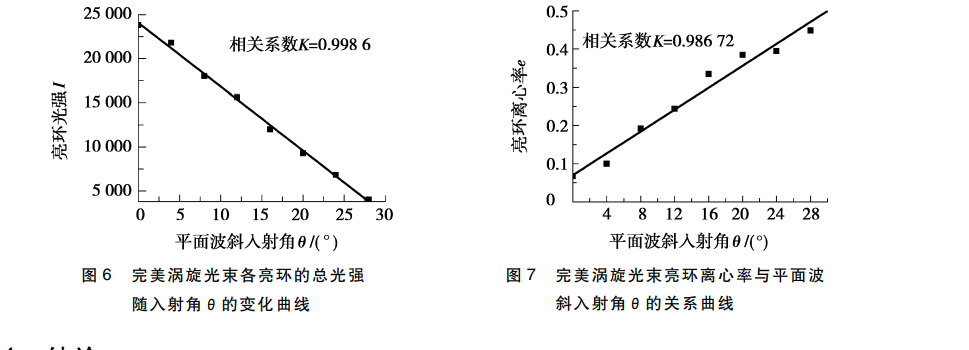
分析图 5 可知：随着平面波斜入射到 SLM的角度在 0°～28°逐渐增大，生成的完美涡旋光束亮环的 光强逐渐减弱，造成这种现象的主要原因是菲涅耳（Fresnel）反射原理。在菲涅耳公式的讨论中[1 8] ，将 入射光分解为电矢量垂直于入射面和平行于入射面的 s 波和 p 波，当光从光疏介质射到光密介质时，s 波和 p 波的反射系数和透射系数随着入射角 θ的增大而减小，所以生成的完美涡旋光束亮环的光强也 随着入射角 θ的增加而减弱。为了更直观地分析生成的完美涡旋光束亮环的光强变化情况，绘制出各 亮环的总光强与入射角 θ的变化曲线，如图 6 所示。由图 6 可知：完美涡旋亮环光强 I 与平面波入射到 SLM的角度 θ呈线性关系，线性函数为 I ＝24 068 -724.58θ。为了量化其线性相关程度，计算了该拟合 公式的相关系数 K，表达式如下：

分析图 5 还可以看出：当平面波入射到 SLM的角度在 0°～28°逐渐增大时，产生的完美涡旋光束亮 环离心率明显增大。当平面波斜入射角大于 28°时，CCD 相机已无法清晰记录产生的完美涡旋光束光 强图。为找出平面波入射角 θ与完美涡旋光束离心率的关系，绘制完美涡旋光束离心率 e 随着平面波 斜入射角 θ的关系曲线，如图 7 所示。由图 7 可以看出：当 θ从 0°增加到 28°时，生成的完美涡旋光束亮 环的离心率从 0.067 4 增加到 0.448 4。通过 Origin 软件拟合可得，完美涡旋光束亮环离心率 e 与平面 波斜入射角 θ呈线性关系。线性函数为 e ＝0.070 11 ＋0.014 33θ，相关系数为 0.986 72，线性拟合度较 好。

4 结论

随着平面波斜入射到 SLM的角度在 0°～28°逐渐增大时，完美涡旋光束亮环光强 I 及完美涡旋光 束离心率 e 均 与 其 呈 线 性 关 系。关 系 式 分 别 为：I ＝24 068 -724.58θ，相 关 系 数 为 0.998 6；e ＝ 0.070 11 ＋0.014 33θ，相关系数为 0.986 72。此外，由于完美涡旋光束光强随 θ增加而减弱，当平面波 斜入射 SLM的角度大于 28°时，CCD 相机无法清晰记录产生的完美涡旋光束。该技术为设计产生完美 涡旋光束的实验光路提供了依据。